二进制、原码、反码、补码
二进制知识了解学习
超出数据类型给定范围的问题
例如:byte数据类型的范围是-128-127
- 看下下面的demo
public class Demo {
public static void main(String[] args) {
//byte能接收的数值范围是-128-127
//给byte赋值为129会报错,但是可以进行强转。128有点特殊
byte num = (byte) 129;
//打印输出的结果是-127
System.out.println(num);
}
}为什么会打印输出成-127呢,我们就需要了解一下二进制,原码,补码相关的一些知识。
二进制
我们最熟悉的是十进制,就是逢十进一。
由此可以推导出二进制的运算,就是逢二进一。
二进制就是由0和1组成的。我们前面讲过数据在内存中存储的形式就是二进制的。
学习二进制有助于我们学习底层的东西,尤其是底层中的变量,以及二进制和其他进制相转换,如二进制,十进制,八进制,十六进制之间的转化。
什么是二进制?
二进制就是由0和1组成的数字序列。
不管什么数字转换成二进制都是0和1组成的。对于计算机而言,数据的存储都是二进制的形式。
| 十进制 | 二进制 | 十进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 17 | 10001 |
| 1 | 1 | … | … |
| 2 | 10 | 31 | 11111 |
| 3 | 11 | 32 | 100000 |
| 4 | 100 | 33 | 100001 |
| 5 | 101 | … | … |
| 6 | 110 | 63 | 111111 |
| 7 | 111 | 64 | 1000000 |
| 8 | 1000 | 65 | 1000001 |
| 9 | 1001 | … | … |
| … | … | 127 | 1111111 |
| 15 | 1111 | 128 | 10000000 |
| 16 | 10000 | … |
我们可以发现如下规律:
- 十进制下每逢2的次幂的数 所对应的 二进制的最高位都是1,其他位都是0,是2的几次幂,就有几个0.
二进制转换为十进制
举个栗子:对于二进制数1011
- 左边是高位,右边是低位,是从右向左
- 第一位表示的是有1个1,第二位表示的是由1个2,第三位表示的是有0个4,第四位表示的是有1个8
- 1+2+0+8=11,所以1011转化为十进制就是11
十进制转换为二进制
总结:“除以2,余数逆序排列”
举个栗子:
- 11转化为二进制
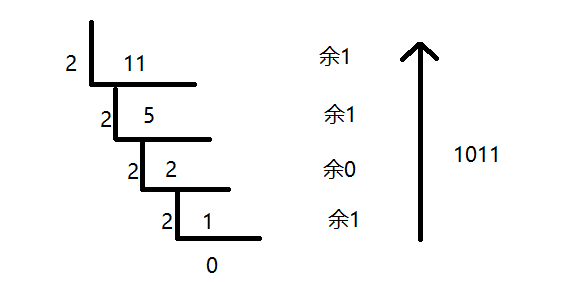
以后用的时候可以用工具直接转,但是现在要明白是什么。
原码,反码,和补码的案例分析
原码反码和补码
-
这是很重要的基础知识,后面如果学JDK源码知识的时候,我们会发现里面就用到了这些。
-
区分正数和负数
- 比如5和-5,正数和负数它们的原码、反码、补码是有区别的。
- 二进制简单来说就是0和1的组合,无论原码,反码,还是补码,他们都是二进制的形式
- 正数是比较简单的,它的原码、反码和补码都是一样的
原码
- 正数
- 对于正数,我们把它的绝对值的二进制数就叫做正数的原码。
- 例如byte类型的5:(byte类型是占一个字节=8bit,也就是8位)
- 5的绝对值:5;5的二进制数:0000 0101 (不够用0补上;5的原码)
因为正数的绝对值还是它本身,所以正数的原码,反码和补码都是一样的,也就是它本身的二进制数。
- 负数
先介绍一下什么是符号位:
-
二进制数的最左边的那一位是符号位,表示这个数是正数还是负数 ,如果是0,表示正数。如果是1,表示负数。
-
例如刚才的5,它是0000 0001 就表示它是正数。
-
对于负数,我们把它的绝对值转化成二进制数,然后最高位补1,得到的二进制数就叫做它的原码
-
例如:-5。它的绝对值是 5,二进制数:0000 0001,最高位补1后:1000 0101 (-5的原码)
反码
反码是在原码的基础上改变而来的!
- 什么是反码?
- 正数的原码反码补码都是一样的
- 负数的反码是对该数的原码 除了符号位 进行取反 得到的二进制数
-5的原码:1000 0101
-5的反码:1111 1010
补码
-
原码->反码->补码:他们都是依据前一个进行改变的。
-
补码的出现主要是解决负数的计算,计算机中存储的都是二进制的补码
-
什么是补码呢?
-
正数的原码反码补码都是一样的
-
负数的补码是对该数的反码的最后一位加1
-
-5的反码:1111 1010
-
-5的补码:1111 1011
扩展问题
byte num = (byte) 129 ; 为什么输出结果是-127?
我们来自己求一下:
-
129是个正数,所以它的原码、反码、补码都是一样的。
-
129的二进制(原码、反码、补码):1000 0001
-
无论是正数还是负数,他们在计算机当中的存储形式都是以补码的形式。因为对于负数,负数在计算机中的存储形式是补码的形式的,我们为了统一,我们可以说成正数和负数在计算机中都是补码的形式,因为正数对于原码反码补码都是一样的。
-
对于129是超出byte的范围的,如果用short存储,short是2个字节,就可以存储:0000 0000 1000 0001。最高位就是0代表正数。
-
但是现在强制转为8位,就变成了 1000 0001.这个就是它的补码。
- 最高位是1,说明是负数
- 知道补码求反码,再求原码,再由原码,再求出这个数的绝对值的二进制数,然后就可以求出打印出的数是多少了
补码:1000 0001 求反码(反码最后一位+1而来,补码最后一位减一回去)
反码:1000 0000 求原码(原码除了符号位取反而来,反码除了符号位取反回去)
原码:1111 1111
这个数的绝对值的二进制数(把最高位换成0):0111 1111
转为十进制是:127 .但是这个是这个数的绝对值的二进制数,我们知道补码的最高位是1,所以是个负数。输出就是-127。
小试牛刀
- 130
-
byte num = (byte) 130;
-
130的正常是:0000 0000 1000 0010
现在强制转换为8位:1000 0010(补码);
补码:1000 0010
反码:1000 0001
原码:1111 1110
-
绝对值的二进制数:0111 1110
-
算出126,因为原补码的最高位为1,所以是负数,就是-126
- 128
-
byte num = (byte) 128;
-
128正常是0000 0000 1000 0000
-
现在强制转化为8位:1000 0000(补码)
补码:1000 0000
反码:0111 1111
原码:0000 0000
-
绝对值的二进制数:0000 0000
-
因为补码的最高位为1,所以这个数是-0???
-
+0代表真的0,而-0代表的是-128.
-
至于为什么8位是-128~127,是由于最高一位存储符号位,所以剩下7位代表数值大小,能从0表示到127
-
所以能从-127表示到127,但由于+0和-0都代表0,重复了,所以,多出一个位子,放到负数,让-0代表-128。
-
所以byte的范围是-128~127。
快速求一个负数的补码
如果我们能用公式快速把一个负数的补码求出来的话,那反过来,如果我们知道这个数的补码的话,我们就可以根据公式,反推出这个负数是多少了。
公式
公式:模+(该负数) = 该负数补码的绝对值数
- 模
- 比如-127,byte是-128到127是可以存下的。而byte是8位的,模的计算方式就是2的n次幂,这个n就是多少位,所以就是2的8次幂等于256。
用8位存储的话,这个模就是256
-
256-127=129,就是该负数补码的绝对值数。
-
算出负数补码:(就是129的二进制数):1000 0001
- 现在反过来:现在想打印byte 129的数是多少
-
129对应的二进制:1000 0001.由于最高位是1,所以推断出是个负数。
-
然后用256-129=127,因为是个负数,所以就是-127
小试牛刀
- byte 130
130 - 256 = -126
- byte 128
128-256 = -128

